Định nghĩa về tam giác đều, tính chất và diện tích tam giác đều

Tam giác đều là một hình học được giáo dục từ môn toán phổ thông khá sớm. Ứng dụng của tam giác đều trong cuộc sống không hề ít. Cũng chính vì thế mà công thức tính diện tích tam giác đều được phổ cập, cần phải ghi nhớ. Bài viết này HP Connect sẽ giúp bạn hiểu hơn về tam giác đều cũng như cách tính diện tích của chúng.

Định nghĩa về tam giác đều

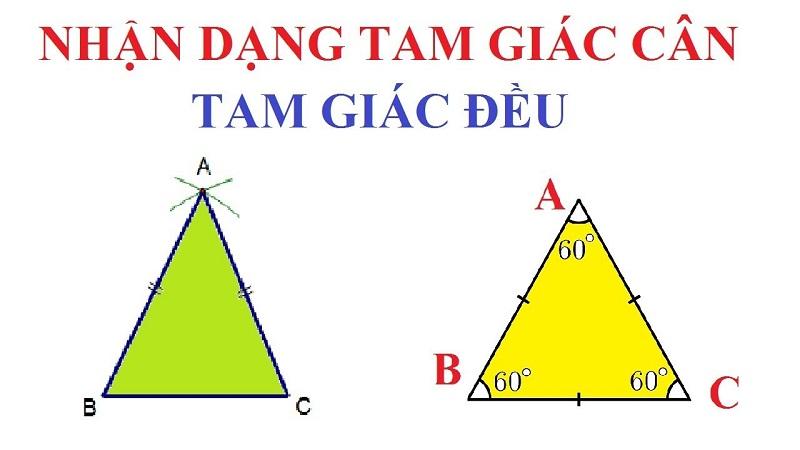
Trong hình học, chúng ta có rất nhiều loại tam giác khác nhau và chúng đều có tính chất, cách nhận biết riêng biệt. Đối với tam giác đều cũng vậy, đây là một tam giác có ba cạnh bằng nhau. Và cũng vì thế mà ba góc của tam giác cũng bằng nhau, đều bằng 60 độ.

Ví dụ, đó là tam giác đều ABC, lúc này cạnh AB = BC = AC. Tổng số đo 3 góc là 180 độ, mỗi góc có số đo 60 độ. Vì tính chất các cạnh, các góc đều bằng nhau nên người ta gọi đó là tam giác đều.

Từ định nghĩa đó chúng ta có thể kết luận, ABC là tam giác đều khi:

• Mỗi góc của tam giác có số đo là 60 độ.
• Một tam giác có ba góc bằng nhau thì đó chính là tam giác đều.
• Tam giác cân có hai cạnh bằng nhau và có 1 góc bằng 60 độ thì đó là tam giác đều.

Tính chất của tam giác đều

Nếu như bạn vẫn còn nhớ bài học tính diện tích tam giác đều lớp 6 thì bạn sẽ được học tất cả những tính chất của tam giác này. Từ đặc điểm của tam giác đều như trên, chúng ta dễ dàng nhận ra tính chất đó là:

• Trong một tam giác đều mỗi góc đều bằng 60 độ. Khi muốn chứng minh diện tích tam giác đều đây là một yếu tố quan trọng.
• Nếu một tam giác có ba cạnh bằng nhau chắc chắn đó là tam giác đều.
• Tam giác cân sẽ trở thành tam giác đều khi có 1 góc bằng 60 độ.
• ĐƯờng cao, đường phân giác của tam giác đều cũng chính là đường trung tuyến của tam giác đó. Ví dụ, tam giác đều ABCD có đường thẳng AH là đường trung tuyến thì đoạn thẳng AH cũng chính là đường cao và đường phân giác (Đường chia góc trong của tam giác thành hai phần bằng nhau.

Đây là những tính chất cực kỳ quan trọng của tam giác đều mà chúng ta cần ghi nhớ. 

Đây là những tính chất vô cùng quan trong để các em có thể áp dụng vào bài tập. Vì vậy các em hãy ghi nhớ thật kỹ 5 tính chất của tam giác đều trên đây. Để có thể áp dụng giải bài tập một cách tốt nhất.

>>> Xem ngay thông tin hữu ích khác:

• Hình bình hành là gì? Cách tính diện tích hình bình hành nhanh nhất
• Tam giác vuông là gì? Cách tính diện tích tam giác vuông chuẩn xác
• Hình thang là gì? Cách tính diện tích hình thang chuẩn xác nhất

Các công thức tính diện tích tam giác đều, chu vi tam giác đều

Trong cuộc sống, tam giác đều được ứng dụng trong rất nhiều lĩnh vực khác nhau và lẽ dĩ nhiên, công thức tính diện tích tam giác đều hay chu vi của nó cực kỳ quan trọng. Thực tế, công thức này đều đã được học ở chương trình giáo dục phổ thông. Tuy nhiên, không phải ai cũng còn nhớ cho tới thời điểm hiện tại. HP Connect sẽ giúp bạn điểm lại những cách tính cơ bản đó nhé.

• Công thức tính diện tích hình tam giác đều: 

• Công thức tính chu vi của tam giác đều: P = 3a

Đây là những công thức quan trọng, dễ nhầm lẫn nên người dùng phải thất sự cẩn thận. bạn cần ghi nhớ chính xác từng công thức để có thể áp dụng vào bài tập và trong cuộc sống. Chắc chắn, bạn sẽ phải thường xuyên sử dụng đến những công thức này.

Làm thế nào để chứng minh được một tam giác là tam giác đều?

Muốn chứng minh một tam giác là tam giác đều chúng ta phải chỉ ra được các tính chất của tam giác đó. Vì thế, bạn cần phải chứng minh tam giác đó có 3 cạnh bằng nhau hoặc ba góc bằng nhau. Chứng minh tam giác này có đường cao chính là đường phân giác và đường trung tuyến. Hoặc bạn cũng có thể chứng minh rằng đây là một tam giác c ân và có 1 góc bằng 60 độ.

Ứng dụng của tam giác đều trong đời sống

Chúng ta đều biết tam giác đều là một dạng hình học quá quen thuộc và phổ biến trong cuộc sống con người. Đó là lý do vì sao mà dạng tam giác này lại được đưa vào chương trình giáo dục phổ thông từ rất sớm. Chúng có thể được ứng dụng để làm đồ chơi cho trẻ em, trang trí không gian kiến trúc, thiết kế nội thất,…

Ứng dụng của tam giác đều với cuộc sống rất đa dạng nên nó cũng được mọi người chú ý đến cách tính diện tích tam giác đều. Chẳng hạn, khi bạn xây dựng một ngôi nhà, bạn dùng cấu trúc tam giác đều để thiết kế một khu vườn trang trí. Bạn phải biết cách tính diện tích tam giác đều này để cân đối về vật liệu cần chuẩn bị, lượng nước sơn, không gian xây dựng,…

Như vậy, chuyên gia công nghệ HP Connect đã giúp bạn nhớ lại công thức tính diện tích tam giác đều cũng như các tính chất của nó. Chắc chắn, khi ghi nhớ thông tin này nó sẽ trở nên vô cùng hữu ích đối với bạn trong cuộc sống. Muốn tính được diện tích tam giác đều nhanh, ít nhất bạn phải có những thông số như là chiều cao, độ dài của cạnh.